刷题,就得按照专题刷。
二叉树,其构成为一个根节点,且必定有两个子节点。在最下面的叶子层全都是为空的子节点。
那么每次以其左子树和右子树作为操作单位,就很自然的将整个树拆分成了更小的树,并且可以结合最后的叶子节点层全都是Null来进行递归的结束判定,可以说树这个结构是天然适合递归的。
参考:https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode%20%E9%A2%98%E8%A7%A3%20-%20%E6%A0%91.md
在大佬的基础之上将一些题目的解法做了更简化的扩展,有些题目的解法,大佬将很多步骤缩成一步,太过简练,我在此将其进行扩展发散,尽量每一步只做一个操作,让大家看的更清楚一些。
面向大佬警告:不是时间最优,不是效率最优,只是便于理解的代码版本,请各位大佬高抬贵手……
打*的是笔者自己做不出来的题目,标记好来再次刷。打&的是最好再回顾一次的题目。
注:2020/08/19作者进行再一次修改,将时间空间复杂度分析放上。
框架
框架分为几种:
- 纯粹递归,一个函数就好:
public int example(TreeNode root){
if(root==null) return 0;
//Here is some operation on TreeNode
//...
//Here is some operation on leftNode and rightNode, depends on problem,like:
L=example(root.left);
R=example(root.right);
return Math.max(L+R)+1;
}
-
并不是越递归就越靠近结果的题目,那么需要保存之前的状态和当前的状态相比较(不然直接每次取当前状态就好),需要一个外部函数触发/检验/返回结果(但是绝对不参与递归!),而一个helper函数做具体的递归工作。
这种情况之中,helper函数的工作一般有:
- 验证是否已经循环结束,比如
if(root==null) - 调用下一次循环并且记录结果,二叉树顶多两个分支,所以一个L一个R足矣。
- 更新外部状态变量result
- 返回其本质的结果,比如求高度就返回高度这些。
- 验证是否已经循环结束,比如
private int result=0;
public int example(TreeNode root){
helper(root);
return result;
}
public int helper(TreeNode root){
if(root==null) return 0;
int L = helper(root.left);
int R = helper(root.right);
result = Math.max(L+R,result);
return Math.max(L,R)+1;
}
递归
1. 树的高度 Maximum Depth of Binary Tree
104 Maximum Depth of Binary Tree
https://leetcode.com/problems/maximum-depth-of-binary-tree/description/
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7return its depth = 3.
代码:
public int maxDepth(TreeNode root) {
if(root==null) return 0;
int left = maxDepth(root.left);
int right =maxDepth(root.right);
return Math.max(left,right)+1;
}
注:框架修改
如果想要在一样的框架下面也解决最短路径问题,可以加上对某一个子树为空的情况判断这一步,参见10 树的最短路径:
class Solution {
public int maxDepth(TreeNode root) {
if(root==null) return 0;
int left = maxDepth(root.left);
int right =maxDepth(root.right);
if(left == 0 || right ==0) return left+right+1;
return Math.max(left,right)+1;
}
}
时空复杂度
时间复杂度:递归需要遍历所有的节点,所以此处为O(n),其中n为二叉树节点的个数。
空间复杂度:O(h),h为树的高度。递归函数需要的是栈空间,而栈空间取决于递归的深度。在二叉树之中,递归的深度就是树的高度。
2. 是否平衡二叉树 Balanced Binary Tree
110 Balanced Binary Tree
这个题目就要借助额外的助手函数了(这是我自己起的名字,意为真正承担逻辑的函数,相比之下题目本身给的函数只是一个入口,我自己叫他入口函数嘿嘿)。
每次要将左边和右边的子树的高度求出,还要将状态做修改,对于只有一个返回值的函数是不够的。那么就再搞出一个函数,作为专门返回状态的函数,而助手函数用来做树的深度的判断和修改这个状态。最后由入口函数返回这个状态的参数。
https://leetcode.com/problems/balanced-binary-tree/description/
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:
Given the following tree
[3,9,20,null,null,15,7]:3 / \ 9 20 / \ 15 7Return true.
class Solution {
boolean res = true;
public boolean isBalanced(TreeNode root) {
dfs(root);
return res;
}
public int dfs(TreeNode root){
if(root == null) return 0;
int left = dfs(root.left);
int right = dfs(root.right);
if(Math.abs(left-right)>1) res = false;
return 1+Math.max(left,right);
}
}
时空复杂度
时间复杂度:O(nlogn),因为每个节点都得调用一下求高度的函数,而且求高度的函数是递归,其深度就是O(logn),每个节点都来一下就是O(nlogn)。
空间复杂度:O(h),其中h是树的高度。又是和上面一样的递归栈。
优化的解法(提前短路)
下面是一种优化的解法,先判断一下到底要不要进行下一轮的递归,如果需要再继续做。不需要的话就直接返回。
为什么短路算法的isBalanced不需要再度判断或者递归?
让我们解析一下maxDepth在自身递归之中的作用:
- 如果传入的是一个空的TreeNode,那么其返回值就是0,会落到最后一个
Math.max语句之中,参与下一次高度的计算 - 如果L或者R是-1,代表其已经有某一部分不符合条件,所以可以直接返回-1到上层进行下一次的返回
- 如果L和R的差值大于1,说明其已经不是一个合格的平衡二叉树,那么需要开始返回-1以便上层调用栈返回-1。
综合以上几点,可以看到其根本就不需要isBalanced再做递归,其已经完成了自己的逻辑闭环。
class Solution {
public boolean isBalanced(TreeNode root) {
if(maxDepth(root)==-1) return false;
return true;
}
public int maxDepth(TreeNode root){
if(root==null) return 0;
int leftCheck = maxDepth(root.left);
if(leftCheck==-1) return -1;
int rightCheck = maxDepth(root.right);
if(rightCheck==-1) return -1;
if(Math.abs(leftCheck-rightCheck)>1) return -1;
return Math.max(leftCheck,rightCheck)+1;
}
}
时空复杂度
时间复杂度:O(n),因为没有了调用这一环,所以每个节点都执行就是O(n)。
空间复杂度:还是O(h),递归还是确实存在的,其深度也就是高度。
3. 树的两节点之间的最长路径
543 Diameter of Binary Tree
此处的逻辑和上面的几乎相同,只是每次做个判定,是否将depth这个值做更新。
https://leetcode.com/problems/diameter-of-binary-tree/description/
Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
Example: Given a binary tree
1 / \ 2 3 / \ 4 5Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
Note: The length of path between two nodes is represented by the number of edges between them.
class Solution {
int depth = 0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return depth;
}
public int depth(TreeNode root){
if(root == null) return 0;
int left = depth(root.left);
int right = depth(root.right);
depth = Math.max(depth,left+right);
return 1+Math.max(left,right);
}
}
时空复杂度
时间复杂度:O(n),每个节点都会被访问到一次
空间复杂度:O(h),因为其函数为递归,而递归的深度就是树的高度。
4. 反转树
226 Invert Binary Tree
结束逻辑:节点是null
拆分更小的问题:将左子树和右子树分别代入
看看,是不是和一开始的想法完全一样?
https://leetcode.com/problems/invert-binary-tree/description/
Invert a binary tree.
Example:
Input:
4 / \ 2 7 / \ / \ 1 3 6 9Output:
4 / \ 7 2 / \ / \ 9 6 3 1
class Solution {
public TreeNode invertTree(TreeNode root) {
helper(root);
return root;
}
public void helper(TreeNode root){
if(root == null) return;
TreeNode tem = root.left;
root.left = root.right;
root.right = tem;
helper(root.left);
helper(root.right);
}
}
*5 合并两棵树
617 Merge Two Binary Trees
本题之中我的想法一开始有问题,总是想着在当前的数据上面修修补补,以至于需要考虑的情况很多。
本题之中要想明白所给的public TreeNode mergeTrees(TreeNode t1, TreeNode t2) 语义是什么,实际上返回值就是t1和t2合并之后的那个节点。
那么本题之中使用递归,就可以得到:
返回条件仍然是两个输入值都为null,其也意味着两棵树都遍历结束了。如果其中一个为null,那么就返回另一个值。两者都不是null,那么先新建一个Node,在其中赋值两者的和,最后在左边叶子和右边叶子上面使用递归即可。
注(2020-09-22):
在看了labuladong的公众号之后,尝试使用”相信递归函数语义 + 分解成每个节点做什么 + 使用前中后序递归框架“ 的思路来做,尝试代码如下:
class Solution { public boolean hasPathSum(TreeNode root, int sum) { if(root==null){ if(sum==0) return true; else return false; } return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val); } }但是遇到这个测试样例通不过:
[] 0 预期结果:false如果一个树是空的,那么这种情况的预期的确应该是false,毕竟什么都没有。对于这种情况,应该加上对节点的和其左右子树的判断。
class Solution { public boolean hasPathSum(TreeNode root, int sum) { if(root==null) return false; if(root.val == sum && root.left == null && root.right == null) return true; return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val); } }
https://leetcode.com/problems/merge-two-binary-trees/
Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.
You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.
Example 1:
Input: Tree 1 Tree 2 1 2 / \ / \ 3 2 1 3 / \ \ 5 4 7 Output: Merged tree: 3 / \ 4 5 / \ \ 5 4 7Note: The merging process must start from the root nodes of both trees.
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if(t1==null && t2==null) return null;
if(t1==null) return t2;
if(t2==null) return t1;
TreeNode root = new TreeNode(t1.val+t2.val);
root.left = mergeTrees(t1.left,t2.left);
root.right = mergeTrees(t1.right,t2.right);
return root;
}
& 6. 判断路径和是否为某个数
112 Path Sum
https://leetcode.com/problems/path-sum/
本题还是使用从上到下的递归。由于题目之中说明一定要到叶子节点才可以算一条链路完成,所以每次从上到下减一层,就对这一层的节点使用public boolean hasPathSum(TreeNode root, int sum-root.val)这种形式的判断。
递归的结束条件总是root==null 的时候要做什么操作。那么本题从语义上看,root为null的时候才返回,自然是前面的节点不满足条件,那么应当返回false。
当这个节点是叶子节点的时候,且值和root.val相同,那么就应该返回true。判断就是root.val == sum && root.left ==null && root.right == null。
最后只要有一条就好,所以使用||来对两个分支做递归操作。
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and
sum = 22,5 / \ 4 8 / / \ 11 13 4 / \ \ 7 2 1return true, as there exist a root-to-leaf path
5->4->11->2which sum is 22.
public boolean hasPathSum(TreeNode root, int sum) {
if(root==null) return false;
if(root.val == sum && root.left ==null && root.right == null) return true;
return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val);
}
7. 统计路径和等于一个数的路径数量
437 Path Sum III
https://leetcode.com/problems/path-sum-iii/
2020-10-01 注:
此处有一个问题,就是我一般习惯了在第一个入口函数的地方传入null的时候,返回对应的结果值result。而按照大佬的解法:
int result = 0; public int pathSum(TreeNode root, int sum) { if (root == null) return 0; result = pathSumStartWithRoot(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum); return result; } private int pathSumStartWithRoot(TreeNode root, int sum) { if (root == null) return 0; int ret = 0; if (root.val == sum) ret++; ret += pathSumStartWithRoot(root.left, sum - root.val) + pathSumStartWithRoot(root.right, sum - root.val); return ret; }如果我将第一个
pathSum()的返回值从return 0变成return null,那么如果正确结果是3,就会返回9。原因是在更新值的时候,之前的值并不会被清除,哪怕pathSum(root.left, sum)是0,其返回的也是之前的result,就会出现三倍的结果的状态。因此在返回值的考量处应当想清楚,不要陷入思维定势。
本题之中的入口函数不仅仅是承担一个拥有返回值的作用了,其还起到了递归的作用。
对于这种从任意一个节点开头到任意一个节点结尾的题目来说,一般是要两个函数:一个题目给的入口函数做不同根的递归,一个自己的helper函数来做以某个TreeNode作为根的情况下的从根到最后的梳理,如果有符合情况的值就将最终的返回值+1。
对于这两个函数而言,其都是需要以root==null为最终的结束,一个是作为外部不同根的递归结束,一个是作为同一个根递归到了叶子节点的递归结束。
You are given a binary tree in which each node contains an integer value.
Find the number of paths that sum to a given value.
The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).
The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.
Example:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8 10 / \ 5 -3 / \ \ 3 2 11 / \ \ 3 -2 1 Return 3. The paths that sum to 8 are: 1. 5 -> 3 2. 5 -> 2 -> 1 3. -3 -> 11
class Solution {
public int result = 0;
public int pathSum(TreeNode root, int sum) {
//不同根的递归
if(root==null) return result;
helper(root,sum);
pathSum(root.left, sum);
pathSum(root.right,sum);
return result;
}
public void helper(TreeNode root, int sum){
//同一个根到叶子节点的递归
if(root==null) return;
if(root.val == sum) result +=1;
helper(root.left,sum-root.val);
helper(root.right,sum-root.val);
}
}
8. 判断一棵树是否为另一颗的子树
572 Subtree of Another Tree
https://leetcode.com/problems/subtree-of-another-tree/
本题之中和上一个题目思想类似,都是一个入口函数分不同根递归,一个帮手函数按照根相同来做判断。
当然,递归肯定要有出口。一般这种参数为两个TreeNode的题目,出口都极其相似,分别是:
- 二者都为null,一般是满足条件的。因为既然都遍历到null了, 说明前面没问题,可以返回true。而且本题说了,给的是两个非空的树(Given two non-empty binary trees s and t, ),就怕你在这纠结null是不是null的子树了。
- 二者其中一个为null。结合前面的二者全是null就返回,那么此处二者一定不全是null。那么二者一定不一样了(我都遍历完了你还没有),一般是不满足条件。
- 这个部分一般没有固定要求,但是一定是有返回值的逻辑,普遍来讲是不满足条件(满足条件就接着递归了)。既然两个都不是null,那就按照特定逻辑返回呗?自己比一下值就好了。本题之中是值不等返回null。值相等的时候没法判定,继续递归即可。
Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.
Example 1: Given tree s:
3 / \ 4 5 / \ 1 2Given tree t:
4 / \ 1 2Return true, because t has the same structure and node values with a subtree of s.
Example 2: Given tree s:
3 / \ 4 5 / \ 1 2 / 0Given tree t:
4 / \ 1 2Return false.
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
if(s==null && t==null) return true;
if(s==null || t==null) return false;
return helper(s,t) || isSubtree(s.left,t) || isSubtree(s.right,t);
}
public boolean helper(TreeNode s, TreeNode t){
if(s==null && t==null) return true;
if(s==null || t== null) return false;
if(s.val != t.val) return false;
return helper(s.left,t.left)&&helper(s.right,t.right);
}
}
9. 树的对称
101 Symmetric Tree
https://leetcode.com/problems/symmetric-tree/
本题逻辑也可以放在树的反转,一个比较一个替换即可。
题目只给了具有一个参数的入口函数,显然不够用,没法直接用其递归:判断是否对称,参数就得两个TreeNode, 一个Node的话是没法进行递归的。所以需要我们再给出一个helper函数。
其判断是否结束,是否返回false的逻辑和我们上面说的一样,还是判断其全是Null和一个为null的情况。除此之外,还有二者的值如果不同直接返回false的一个条件。
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
For example, this binary tree
[1,2,2,3,4,4,3]is symmetric:1 / \ 2 2 / \ / \ 3 4 4 3But the following
[1,2,2,null,3,null,3]is not:1 / \ 2 2 \ \ 3 3Follow up: Solve it both recursively and iteratively.
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null) return true;
return helper(root.left,root.right);
}
public boolean helper(TreeNode s, TreeNode t){
if(s==null && t==null) return true;
if(s==null || t==null) return false;
if(s.val!= t.val) return false;
return helper(s.left,t.right) && helper(s.right,t.left);
}
}
* 10. 树的最短路径
111 Minimum Depth of Binary Tree
https://leetcode.com/problems/minimum-depth-of-binary-tree/
本题表星的原因是,我将本题和第一个题目使用了一样的套路,结果失败了。失败原因如下:
在求最长路径的时候,是不需要考虑左边或者右边为null这种情况,因为这种情况相应的递归是0,在使用Math.max(a,b)的过程之中,一个值为0,另外一个如果也是0,意味着其为叶子节点,不需要特殊处理。如果另一个不是0,那么max之中返回的一定是这个不为0的数,也不需要特殊处理。
本题不同。如果不特殊对某个分支为0的情况进行处理,使用下面的代码,就会造成这种情况:
class Solution {
public int minDepth(TreeNode root) {
if(root==null) return 0;
int left = minDepth(root.left);
int right = minDepth(root.right);
//if(left == 0 || right == 0) return left+right+1;
return Math.min(left,right)+1;
}
}
对于一棵只有一个子节点的树,比如 [1,2],1下面的某一个子节点是2。那么如果将上面的代码使用,其left=0,right=1,返回的就是0+1=1. 但是这个是错误的,因为其右边有叶子,如果不计算的话就会造成错误。所以要对这种情况进行单独考察:
class Solution {
public int minDepth(TreeNode root) {
if(root==null) return 0;
int left = minDepth(root.left);
int right = minDepth(root.right);
if(left == 0 || right == 0) return left+right+1;
return Math.min(left,right)+1;
}
}
将注释去掉,可以得到二者之一为0的时候,其返回的就是不为0的值+1. 那么就避免了只有一个子树的情况下错误判断。
Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7return its minimum depth = 2.
11. 左叶子的和
404 Sum of Left Leaves
https://leetcode.com/problems/sum-of-left-leaves/
本题实际上也比较简单,都不需要使用helper函数,直接自己递归就好。同样的,也是判断是否为null来结束。左叶子的判断方法前面有叙述,不再赘述。
Find the sum of all left leaves in a given binary tree.
Example:
3 / \ 9 20 / \ 15 7 There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
class Solution {
int result = 0;
public int sumOfLeftLeaves(TreeNode root) {
if(root==null) return result;
if(root.left!=null && root.left.left==null && root.left.right==null) result+=root.left.val;
sumOfLeftLeaves(root.left);
sumOfLeftLeaves(root.right);
return result;
}
}
* 12. 相同值的最大路径长度
687 Longest Univalue Path
https://leetcode.com/problems/longest-univalue-path/
个人认为这道题的难度不应该是easy。本题之中不能使用之前的模型一应概之,而是需要不同方面考虑。
class Solution {
public int result =0;
public int longestUnivaluePath(TreeNode root) {
sameDepth(root);
return result;
}
public int sameDepth(TreeNode root){
if(root==null) return 0;
int left = sameDepth(root.left);
int right = sameDepth(root.right);
int leftDepth = (root.left!=null && root.val==root.left.val )? left+1:0;
int rightDepth = (root.right!=null && root.val == root.right.val) ? right+1:0;
result = Math.max(result,leftDepth+rightDepth);
return Math.max(leftDepth,rightDepth);
}
}
首先,本题不能直接套用之前的”入口函数递归不同的根,实际函数递归同一个根的树“的规则。如果这样去想,整道题目复杂无比:每次都需要传入一个当前的val和下一个节点,比如当前节点的值和左节点,然后进行比较,相等的话某个值+1;
本题使用的是另外一种思路:
先使用递归求出其左子树,右子树之中符合条件的长度left 和 right。然后定义两个新变量,一个leftPath, 一个 rightPath,其中如果本节点的值和左子树节点的值一样,就leftPath = left+1,和右子树的节点值一样,就rightPath = right+1。不一样的话就赋值为0。最后,让最外层的结果result 和leftPath+rightPath做一个比较,然后,返回值是leftPath和rightPath之中较大的一个。
注意,此处的返回值的意义还是左边/右边和其相同的最长长度,而result是每次和leftPath+rightPath相比较。
* 13. 隔层遍历
337 House Robber III
https://leetcode.com/problems/house-robber-iii/
这个题目,我认为是真的搞到了递归的精髓。对于每一层,不是先直接抢劫,而是计算(抢劫该层+该层的间隔一层)和(抢劫该层的下一层) 哪个收益更大。由于二叉树不能回溯,那么每次其实都是局部最优解——站在该层去看对于该层的选择哪种更好,然后立足于这个更好的结果进行下次选择。
其关键是不能慌,不能到一层先抢了再说,那就很被动了。
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.
Determine the maximum amount of money the thief can rob tonight without alerting the police.
Example 1:
Input: [3,2,3,null,3,null,1] 3 / \ 2 3 \ \ 3 1 Output: 7 Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.Example 2:
Input: [3,4,5,1,3,null,1] 3 / \ 4 5 / \ \ 1 3 1 Output: 9 Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
class Solution {
public int rob(TreeNode root) {
if(root==null) return 0;
int v1 = root.val;
if(root.left!=null) v1+=(rob(root.left.left)+rob(root.left.right));
if(root.right!=null) v1+=(rob(root.right.left)+rob(root.right.right));
int v2 = rob(root.left)+rob(root.right);
return Math.max(v1,v2);
}
}
* 14. 寻找第二小的数
671 Second Minimum Node In a Binary Tree
https://leetcode.com/problems/second-minimum-node-in-a-binary-tree/
这个题目本身给的设计条件很多,不具有普适性。也梳理一下思路,当做后人的参考。
题目本身说了, 每一个节点要么有两个子节点,要么没有子节点。而且每一个节点,都是下面两个节点之中的最小值。这本身就是一个很特殊的二叉树。
那么对于这个二叉树,我们想找到其中第二小的数字。 找不到的话,比如没有子节点,比如所有值都相同(没有第二小的数字),那么就返回-1.
有思路为:
既然根节点一定是两个子节点之中的最小值,那么分情况讨论:
- 如果这个节点A是null,或者其两个子节点B,C是null,直接返回-1
- 如果其有两个子节点B,C,那么肯定和其中至少一个子节点的值是相同的。如果不相同,意味着根节点的值比这个不同的节点的值小,这一分支就不必递归了(递归之后可能会变大)。哪个分支的值和根节点的值相同,就对哪个分支进行下一步的递归,两个都相同,就都进行递归——假设A和B的值相同,那么对以B为根节点的子树进行递归。如果以B为根节点的子树的值都是和B相同,那么其会返回-1.不同的话,则会以第一个比B大的值作为返回值(也是一样的语义,findSecondMinimumValue)。
- 对分支进行递归之后,哪个分支的值是-1,说明其下面的所有值都是和A相同,直接舍弃。如果两个都不是-1,那么比较返回其中的较小值即可。
Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly
twoorzerosub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the propertyroot.val = min(root.left.val, root.right.val)always holds.Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.
If no such second minimum value exists, output -1 instead.
Example 1:
Input: 2 / \ 2 5 / \ 5 7 Output: 5 Explanation: The smallest value is 2, the second smallest value is 5.Example 2:
Input: 2 / \ 2 2 Output: -1 Explanation: The smallest value is 2, but there isn't any second smallest value.
class Solution {
public int findSecondMinimumValue(TreeNode root) {
if(root==null) return -1;
if(root.left == null&& root.right==null) return -1;
if(root.left.val==root.val) root.left.val = findSecondMinimumValue(root.left);
if(root.right.val==root.val) root.right.val = findSecondMinimumValue(root.right);
if(root.left.val == -1 && root.right.val == -1) return -1;
if(root.left.val == -1 && root.right.val != -1) return root.right.val;
if(root.left.val!=-1 && root.right.val == -1) return root.left.val;
return Math.min(root.left.val, root.right.val);
}
}
层次遍历
*15 输出每一层的平均值
637 Average of Levels in Binary Tree
https://leetcode.com/problems/average-of-levels-in-binary-tree/
本题之中,其平均值的求法还是使用层次遍历:每一层的节点相加,然后除以节点的数量。
题目本身之中比较重要的是,使用一个Queue作为TreeNode的暂存位置,循环结束的条件是queue.isEmpty(),在每一层循环之中,都先得到目前的queue的长度,然后取这些长度的节点进行相加,遍历和求平均值,并且放到list里面。在遍历过程之中,如果当前节点的左/右节点不是null,那么就将其放入queue之中。
Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array.
Example 1:
Input: 3 / \ 9 20 / \ 15 7 Output: [3, 14.5, 11] Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].Note:
- The range of node’s value is in the range of 32-bit signed integer.
class Solution {
ArrayList<Double> list = new ArrayList<>();
public List<Double> averageOfLevels(TreeNode root) {
if(root==null) return list;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int counter = queue.size();
double result = 0;
for(int i=0;i<counter;i++){
TreeNode node = queue.poll();
result+=node.val;
if(node.left!=null) queue.add(node.left);
if(node.right!=null) queue.add(node.right);
}
result = result/counter;
list.add(result);
}
return list;
}
}
16. 得到左下角的节点
513 Find Bottom Left Tree Value
https://leetcode.com/problems/find-bottom-left-tree-value/
本题的”左下角“,含义是最下层的最左边的节点。那么还是按照之前的层次遍历,每次只要其下面的节点不是Null,就进行入队。
但是此处的入队顺序要注意,因为我们没法判断哪一层是最后一层(如果使用一个节点的左子节点和右子节点做判断,只能判断出其是不是叶子节点,没法判断这一层是不是最下一层)。而且队列是先入先出,所以只能让最下一层的最左节点最后一个出队。那么在入队的时候,就要对每一层都是先入右子节点,再入左子节点。这样,每次都将结果赋值成当前出队的节点,最后返回的时候就一定是最下一层的最左节点了。
Given a binary tree, find the leftmost value in the last row of the tree.
Example 1:
Input: 2 / \ 1 3 Output: 1Example 2:
Input: 1 / \ 2 3 / / \ 4 5 6 / 7 Output: 7Note: You may assume the tree (i.e., the given root node) is not NULL.
class Solution {
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue= new LinkedList<>();
queue.add(root);
TreeNode result = root;
while(!queue.isEmpty()){
int size = queue.size();
for(int i=0;i<size;i++){
TreeNode node = queue.poll();
result = node;
if(node.right != null) queue.add(node.right);
if(node.left != null) queue.add(node.left);
}
}
return result.val;
}
}
前中后序遍历
左右子节点的顺序一定是先左后右,那么这个前中后序指的是什么呢?指的是根节点的顺序。
- 根-左-右:前序
- 左-根-右:中序
- 左-右-根:后序
每一种情况还都分为递归和非递归。如果递归的话,三种写法几乎相同。
① 前序
void dfs(TreeNode root) {
visit(root);
dfs(root.left);
dfs(root.right);
}
② 中序
void dfs(TreeNode root) {
dfs(root.left);
visit(root);
dfs(root.right);
}
③ 后序
void dfs(TreeNode root) {
dfs(root.left);
dfs(root.right);
visit(root);
}
此处介绍的是非递归写法。
17. 前序遍历的非递归写法
144 Binary Tree Preorder Traversal
https://leetcode.com/problems/binary-tree-preorder-traversal/description/
普遍认为,前序遍历的非递归是最好写的。写法为借助一个栈,先入栈根,然后出栈并记录之,按照:右节点和左节点的顺序进行入栈。当然要判断当前节点是否为空。
如果当前节点非空,且栈非空,继续循环直到结束。
Given a binary tree, return the preorder traversal of its nodes’ values.
Example:
Input: [1,null,2,3] 1 \ 2 / 3 Output: [1,2,3]Follow up: Recursive solution is trivial, could you do it iteratively?
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if(root==null) return list;
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
list.add(node.val);
if(node.right!=null) stack.push(node.right);
if(node.left!=null) stack.push(node.left);
}
return list;
}
}
* 18. 中序遍历的非递归写法
94 Binary Tree Inorder Traversal
https://leetcode.com/problems/binary-tree-inorder-traversal/
本题的解法是借助一个栈。其中对于指向当前节点的指针使用比较精妙。另外还需要两层while来循环整个过程。
中间一层while:每次先将当前节点入栈,如果当前节点有非空左子节点,入栈,并且将当前节点指针指向非空左子节点。
外面一层while:条件为当前节点指针非空,或者栈非空。在第一波将所有左子节点塞入栈之后,出栈一个节点,记录其值。如果出栈的节点有右子节点,将当前节点指针指向右子节点。
第一层while,也就是外面一层while的原理:当前子节点非空,说明还要继续递归。当前栈非空,说明还有没处理完的节点。
Given a binary tree, return the inorder traversal of its nodes’ values.
Example:
Input: [1,null,2,3] 1 \ 2 / 3 Output: [1,3,2]Follow up: Recursive solution is trivial, could you do it iteratively?
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
ArrayList<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if(root==null) return list;
while(root!=null || !stack.isEmpty()){
while(root!=null){
stack.push(root);
root=root.left;
}
TreeNode node = stack.pop();
list.add(node.val);
root=node.right;
}
return list;
}
}
* 19. 后续遍历的非递归写法
145 Binary Tree Postorder Traversal
https://leetcode.com/problems/binary-tree-postorder-traversal/
本题的原理和前序一样,只是多一步列表翻转。
前序是 根-左-右, 后序是左-右-根。那么如果将前序的遍历顺序变成根-右-左,然后再整体反转结果的返回链表,就能得到左-右-根的这种后序遍历了。
Given a binary tree, return the postorder traversal of its nodes’ values.
Example:
Input: [1,null,2,3] 1 \ 2 / 3 Output: [3,2,1]Follow up: Recursive solution is trivial, could you do it iteratively?
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
ArrayList<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if(root==null) return list;
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
list.add(node.val);
if(node.left!=null) stack.push(node.left);
if(node.right!=null) stack.push(node.right);
}
Collections.reverse(list);
return list;
}
}
根据前中/中后/前后遍历顺序还原二叉树
20. 从前序和中序还原二叉树
105 Construct Binary Tree from Preorder and Inorder Traversal
https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
这种还原二叉树的题目,本质上都是一样的:每次找到根节点是谁,左边子树在对应的序之中是从哪到哪,然后递归即可。每次返回的都只是根节点这个新建节点。
步骤为:
- 找到对应的根节点A,前序的话第一个节点一定是根节点
- 找到左右子树两部分:在中序遍历之中A的左边一定是左子树,右边一定是右子树。
- 递归求解即可。
注意:此处在开始要判断两个数组的长度是否一致/长度是否为0。满足的话直接返回null就好了。至于其中的copyOfRange()为什么可以取下标是1,是因为代码之中写了这个注释:
* @throws ArrayIndexOutOfBoundsException if {@code from < 0}
* or {@code from > original.length}
可见如果一个数组的长度为1,那么是可以执行类似copyOfRange(array,1,1)这样的代码的,其返回值会是一个空的array。
将代码做出改进,发现三种还原之中,如果都对当前数组长度为1的时候进行一个判断并且直接返回值,可能要更好一点。下面的代码也都是加入了相应的判断。
Given preorder and inorder traversal of a tree, construct the binary tree.
Note: You may assume that duplicates do not exist in the tree.
For example, given
preorder = [3,9,20,15,7] inorder = [9,3,15,20,7]Return the following binary tree:
3 / \ 9 20 / \ 15 7
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length!=inorder.length || preorder.length==0) return null;
int head = preorder[0];
int position = findPosition(inorder,head);
TreeNode node = new TreeNode(head);
if(preorder.length==1) return node;
node.left=buildTree(Arrays.copyOfRange(preorder,1,position+1),Arrays.copyOfRange(inorder,0,position));
node.right = buildTree(Arrays.copyOfRange(preorder, position+1,preorder.length),Arrays.copyOfRange(inorder,position+1,inorder.length));
return node;
}
public int findPosition(int[] array, int num){
for(int i=0;i<array.length;i++){
if(array[i]==num) return i;
}
return -1;
}
}
21. 从中序和后序还原二叉树
106 Construct Binary Tree from Inorder and Postorder Traversal
https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
本题和上一个题目几乎全部相同。只是在递归的时候注意一下两个部分的起始点即可。
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder.length==0|| inorder.length!=postorder.length) return null;
TreeNode node = new TreeNode(postorder[postorder.length-1]);
int i=0;
if(inorder.length==1) return node;
for(int j=0;j<inorder.length;j++){
if(inorder[j]==postorder[postorder.length-1]) i=j;
}
node.left = buildTree(Arrays.copyOfRange(inorder,0,i),Arrays.copyOfRange(postorder,0,i));
node.right = buildTree(Arrays.copyOfRange(inorder,i+1,inorder.length),Arrays.copyOfRange(postorder,i,postorder.length-1));
return node;
}
}
22. 从前序和后序还原二叉树
889 Construct Binary Tree from Preorder and Postorder Traversal
思路一样,就不赘述了。
Return any binary tree that matches the given preorder and postorder traversals.
Values in the traversals pre and post are distinct positive integers.
Example 1:
Input: pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1] Output: [1,2,3,4,5,6,7]
Note:
1 <= pre.length == post.length <= 30 pre[] and post[] are both permutations of 1, 2, …, pre.length. It is guaranteed an answer exists. If there exists multiple answers, you can return any of them.
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
class Solution {
public TreeNode constructFromPrePost(int[] pre, int[] post) {
if(pre.length!=post.length || pre.length==0) return null;
TreeNode root = new TreeNode(post[post.length-1]);
int index = 0;
if(pre.length==1) return root;
for(int i=0;i<post.length;i++){
if(post[i]==pre[1]) index = i;
}
root.left = constructFromPrePost(Arrays.copyOfRange(pre,1,index+2),Arrays.copyOfRange(post,0,index+1));
root.right = constructFromPrePost(Arrays.copyOfRange(pre,index+2,pre.length),Arrays.copyOfRange(post,index+1,post.length-1));
return root;
}
}
二叉查找树BST
* 23. 修剪二叉查找树
669 Trim a Binary Search Tree
https://leetcode.com/problems/trim-a-binary-search-tree/
本题之中使用递归,原理是”修剪“,也就是如何不断舍去不要的节点(不断缩小范围)。下文之中L代表区间左值,R代表区间右值。
那么就分几种情况:
- 根节点的值直接大于R,那么相应的从根节点到右子树应该全部舍去,直接在左子树上面开始找。
- 根节点的值直接小于L,那么从根节点到左子树全部舍弃,在右子树上面开始找。
- 根节点的值在L,R之间,那么需要对其左子树和右子树都进行操作:
- 左节点的值直接变成修剪左子树的返回值
- 右节点的值直接变成修剪右子树的返回值
- 最后返回节点即可。
Given a binary search tree and the lowest and highest boundaries as
LandR, trim the tree so that all its elements lies in[L, R](R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.Example 1:
Input: 1 / \ 0 2 L = 1 R = 2 Output: 1 \ 2Example 2:
Input: 3 / \ 0 4 \ 2 / 1 L = 1 R = 3 Output: 3 / 2 / 1
class Solution {
public TreeNode trimBST(TreeNode root, int L, int R) {
if(root==null) return null;
if(root.val>R) return trimBST(root.left,L,R);
if(root.val<L) return trimBST(root.right,L,R);
root.left = trimBST(root.left,L,R);
root.right = trimBST(root.right,L,R);
return root;
}
}
*24. 寻找BST的第k个元素
230 Kth Smallest Element in a BST (Medium)
https://leetcode.com/problems/kth-smallest-element-in-a-bst/
BST中序遍历有序,直接借助这一点进行查找第k个元素。
得借助外面的两个变量,一个存储当前遍历到了第几位,一个存储最终的返回结果。
因为我在递归开始的时候就进行了res++,所以判断条件应该是if(res==k),而不是和k-1做判断。但是,如果是对于借助arrayList来进行结果存储的情况下,需要考虑第n小的元素下标是n-1.
Given a binary search tree, write a function
kthSmallestto find the kth smallest element in it.Note: You may assume k is always valid, 1 ≤ k ≤ BST’s total elements.
Example 1:
Input: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 Output: 1Example 2:
Input: root = [5,3,6,2,4,null,null,1], k = 3 5 / \ 3 6 / \ 2 4 / 1 Output: 3Follow up: What if the BST is modified (insert/delete operations) often and you need to find the kth smallest frequently? How would you optimize the kthSmallest routine?
class Solution {
int res = 0;
int ret=0;
public int kthSmallest(TreeNode root, int k) {
if(root==null) return 0;
inorder(root,k);
return ret;
}
public void inorder(TreeNode node,int k){
if(node ==null) return;
inorder(node.left,k);
res++;
if(res==k){
ret = node.val;
return;
}
inorder(node.right,k);
}
}
*25. 将二叉查找树的每个节点的值都加上比它大的节点的值
538 Convert BST to Greater Tree (Easy)
https://leetcode.com/problems/convert-bst-to-greater-tree/
Given a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.
Example:
Input: The root of a Binary Search Tree like this: 5 / \ 2 13 Output: The root of a Greater Tree like this: 18 / \ 20 13Note: This question is the same as 1038: https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/
解法一
最暴力的解法就是将比一个数字大的所有数字都拿出来,然后相加了。
首先,利用BST的性质,使用一个arrayList来承接按照中序遍历的BST的结果,那么这个arrayList就是天然有序的。
之后,对于每一个TreeNode,找到其在arrayList之中的位置,然后将值变为0(也可以从这个位置往后加来判断,但是这样可能会有边界问题,需要在此判断,我这边省事就直接以0开始)。从这个位置开始向后相加,直到加完,那么一个TreeNode的值就修改好了。
最后,将左右子节点分别这样遍历,最后返回根节点即可。
使用这种方式的时间和空复杂度都较高。
class Solution {
ArrayList<Integer> arrayList = new ArrayList<>();
public TreeNode convertBST(TreeNode root) {
if(root==null) return null;
middleOrder(root);
helper(root);
return root;
}
public void helper(TreeNode root){
if(root==null) return;
int index = 0;
for(int i=0;i<arrayList.size();i++){
if(arrayList.get(i)==root.val) index = i;
}
root.val = 0;
for(int i=index;i<arrayList.size();i++){
root.val+=arrayList.get(i);
}
helper(root.left);
helper(root.right);
}
public void middleOrder(TreeNode node){
if(node ==null) return;
middleOrder(node.left);
arrayList.add(node.val);
middleOrder(node.right);
}
}
* 解法二
根据BST的性质,要去找对于某个节点而言的更大的值,分两种情况:
- 假设这个节点是左子节点,那么比它大的值是这棵树对应的根节点+右子节点
- 假设这个节点是根节点,那么比它大的值是这棵树的右子节点
如果使用一个数字作为累加和,那么应该先对右边子节点的值进行累加,这样可以保证操作的时候针对的节点是根节点和右子节点。然后再对于左边的数字进行遍历,这样就能够对于每个左子节点,加上的值都是右子节点+根的值。
所以整个递归过程之中的第一步,应该是对于整棵树的右子节点进行操作,发现其右子节点是空,进行下一步,对于其根节点进行操作,加上这个右子节点的值……这样往复循环。
class Solution {
int sum =0;
public TreeNode convertBST(TreeNode root) {
helper(root);
return root;
}
public void helper(TreeNode root){
if(root==null) return;
helper(root.right);
sum+=root.val;
root.val = sum;
helper(root.left);
}
}
* 26. BST的最近公共祖先
235 Lowest Common Ancestor of a Binary Search Tree
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/description/
本题之中讲了,是在BST之中搜索最近的公共祖先,一开始笔者冥思苦想,自己认为要借助两个栈,先遍历,然后将路上遇到的节点入栈,最后不断出栈比较这种形式。这种觉得过于繁杂。
下面这个格式很清晰,就是“只要从上到下遍历,看到了在这两个值之间的节点就直接输出”。
按照二叉树对应看了一下, 的确是这样。
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
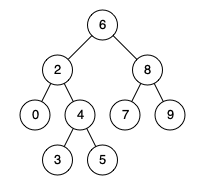
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 Output: 6 Explanation: The LCA of nodes 2 and 8 is 6.Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 Output: 2 Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.Note:
- All of the nodes’ values will be unique.
- p and q are different and both values will exist in the BST.
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return null;
if(root.val<p.val && root.val<q.val) return lowestCommonAncestor(root.right,p,q);
if(root.val>p.val && root.val>q.val) return lowestCommonAncestor(root.left,p,q);
return root;
}
}
* 27 二叉树的最近公共祖先
236 Lowest Common Ancestor of a Binary Tree
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/
说实话,这个题目我拿到是懵逼的,虽然和上面的一个题如此相近,但是这是一个完全没有任何规律的二叉树,也就谈不上使用大小来获取关系了。
在树的递归之中,如何根据不同的场景找到不同的结束条件和返回值是很重要的事情。
本题之中,递归的结束条件有三种:
root==null,意味着这一支已经遍历完毕root==p,意味着遍历到其中一个的值,再往下没有意义root==q,和上面这个一样。
三种递归条件结束都是返回root,即条件满足时候的值。
使用递归框架,用left和right来记录左边递归和右边递归的值。
返回值:
if(right==null),意味着这一支遍历完毕,且最后没有得到值。那么无脑返回left。if(left==null),同上,无脑返回right。- 直接返回root。这种情况下left和right都不是null,那么这个时候root就是要的返回值(二者的根)
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
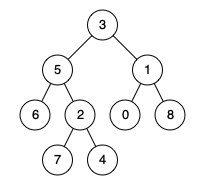
Given the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3.Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.Note:
- All of the nodes’ values will be unique.
- p and q are different and both values will exist in the binary tree.
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null || root==p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(right==null){
return left;
}
if(left==null){
return right;
}
return root;
}
}
* 28. 从有序数组之中构建BST
108 Convert Sorted Array to Binary Search Tree
https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree/description/
题目不仅要求BST,而且要求是 height balanced 的 BST。那么我们就不能做一个类似链表的一样的最简单的BST来提交了。
如何尽量保证高度平衡?因为是有序数组,所以尽量每次都取中间的值来产生TreeNode。
本题之中需要自己写一个helper函数,TreeNode helper(int[] nums, int i,int j)。其中,i是起始值,j是终止值。递归的终止条件,就是当i>j的时候,也就是这个数组之中一个值都没有的时候,就直接返回null了。
Given an array where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Example:
Given the sorted array: [-10,-3,0,5,9], One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST: 0 / \ -3 9 / / -10 5
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return helper(nums,0, nums.length-1);
}
public TreeNode helper(int[] nums, int i,int j){
if(i>j) return null;
int mid = (i+j)/2;
TreeNode root = new TreeNode(nums[mid]);
root.left = helper(nums,i,mid-1);
root.right = helper(nums,mid+1,j);
return root;
}
}
* 29. 从有序链表之中恢复BST
109 Convert Sorted List to Binary Search Tree
https://leetcode.com/problems/convert-sorted-list-to-binary-search-tree/
本题和上一题有些相似,但是链表本身如何判断“中位数”? 答案是使用快慢指针。
由于要以“中位数”为界限进行分割,所以要得到三个位置的ListNode: 中位数之前,中位数,中位数之后:
以中位数为值进行TreeNode的组建,将中位数之前的ListNode的next设置成null,用来分割链表;以中位数之后的ListNode作为递归的两个起点之一。
所以本题之中比较有趣的是ListNode preMid(ListNode head),如其含义所示,preMid,就是Mid之前的ListNode。
且其快慢指针不是同时开始,快指针本来就比慢指针快一步。
Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Example:
Given the sorted linked list: [-10,-3,0,5,9], One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST: 0 / \ -3 9 / / -10 5
class Solution {
public TreeNode sortedListToBST(ListNode head) {
if(head == null) return null;
if(head.next == null) return new TreeNode(head.val);
ListNode preMid = preMid(head);
TreeNode res = new TreeNode(preMid.next.val);
ListNode midNext = preMid.next.next;
preMid.next = null;
res.left = sortedListToBST(head);
res.right = sortedListToBST(midNext);
return res;
}
public ListNode preMid(ListNode head){
ListNode slow = head;
ListNode fast = head.next;
ListNode preMid = head;
while(fast!=null && fast.next!=null){
preMid = slow;
slow = slow.next;
fast = fast.next.next;
}
return preMid;
}
}
30. 二叉树之中寻找两个节点值为一个给定值
653 Two Sum IV - Input is a BST
https://leetcode.com/problems/two-sum-iv-input-is-a-bst/
暴力解法,直接生成有序arrayList然后直接双指针。
大佬还有这样一句评语:
“应该注意到,这一题不能用分别在左右子树两部分来处理这种思想,因为两个待求的节点可能分别在左右子树中。”
Given a Binary Search Tree and a target number, return true if there exist two elements in the BST such that their sum is equal to the given target.
Example 1:
Input: 5 / \ 3 6 / \ \ 2 4 7 Target = 9 Output: TrueExample 2:
Input: 5 / \ 3 6 / \ \ 2 4 7 Target = 28 Output: False
class Solution {
ArrayList<Integer> arrayList = new ArrayList<>();
public boolean findTarget(TreeNode root, int k) {
if(root==null) return false;
middleOrder(root);
int i=0,j=arrayList.size()-1;
while(i<j){
int small = arrayList.get(i);
int big = arrayList.get(j);
if(small+big<k) i=i+1;
if(small+big == k) return true;
if(small+big>k) j=j-1;
}
return false;
}
public void middleOrder(TreeNode root){
if(root==null) return;
middleOrder(root.left);
arrayList.add(root.val);
middleOrder(root.right);
}
}
31 BST之中两个数的最小差值
530 Minimum Absolute Difference in BST
https://leetcode.com/problems/minimum-absolute-difference-in-bst/
中序遍历之后不断比较相邻两个数字差值即可。
Given a binary search tree with non-negative values, find the minimum absolute difference between values of any two nodes.
Example:
Input: 1 \ 3 / 2 Output: 1 Explanation: The minimum absolute difference is 1, which is the difference between 2 and 1 (or between 2 and 3).Note:
- There are at least two nodes in this BST.
- This question is the same as 783: https://leetcode.com/problems/minimum-distance-between-bst-nodes/
class Solution {
ArrayList<Integer> arrayList = new ArrayList<>();
public int getMinimumDifference(TreeNode root) {
if(root==null) return 0;
inorder(root);
int ret = arrayList.get(1)-arrayList.get(0);
for(int i=0;i<arrayList.size()-1;i++){
if(ret>arrayList.get(i+1)-arrayList.get(i)){
ret=arrayList.get(i+1)-arrayList.get(i);
}
}
return ret;
}
public void inorder(TreeNode root){
if(root==null) return;
inorder(root.left);
arrayList.add(root.val);
inorder(root.right);
}
}
*32 寻找BST之中出现次数最多的值
501 Find Mode in Binary Search Tree
https://leetcode.com/problems/find-mode-in-binary-search-tree/
本题之中实际上使用了中序遍历来得到按序排列的元素值,然后在中序遍历的节点处理部分做了具体的逻辑操作。
借助三个外部变量,一个curcnt代表当前的节点的出现次数,一个maxcnt代表已知的节点出现次数,一个TreeNode pre用来存储上一次处理的节点。
那么在实际的逻辑:inorder之中,对于当前节点root的处理逻辑是:
- 如果pre非空,那么比较其和root的关系,如果值相同,那么curcnt+1,如果值不相同,那么直接将curcnt置为1(相当于重新初始化)
- 比较curcnt和maxcnt的关系,如果curcnt>maxcnt,那么将当前的数组清零,maxcnt=curcnt,且将当前节点的值塞入arrayList。如果相等,那么直接将值塞入arrayList即可。
- 最后将pre=root,即每次都要更新节点。
Given a binary search tree (BST) with duplicates, find all the mode(s) (the most frequently occurred element) in the given BST.
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
- Both the left and right subtrees must also be binary search trees.
For example: Given BST
[1,null,2,2],1 \ 2 / 2return
[2].Note: If a tree has more than one mode, you can return them in any order.
Follow up: Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
class Solution {
int curcnt = 1;
int maxcnt = 1;
TreeNode pre = null;
public int[] findMode(TreeNode root) {
ArrayList<Integer> arrayList = new ArrayList<>();
inorder(root,arrayList);
int[] res = new int[arrayList.size()];
for(int i=0;i<arrayList.size();i++){
res[i]=arrayList.get(i);
}
return res;
}
public void inorder(TreeNode root, List<Integer> nums){
if(root==null) return;
inorder(root.left,nums);
if(pre!=null){
if(pre.val==root.val){
curcnt+=1;
}else{
curcnt=1;
}
}
if(curcnt>maxcnt){
nums.clear();
maxcnt=curcnt;
nums.add(root.val);
}else if(curcnt==maxcnt){
nums.add(root.val);
}
pre = root;
inorder(root.right,nums);
}
}
33. 序列化和反序列化二叉树
449 Serialize and Deserialize BST
本题我采用的是层序遍历。因为空的节点在序列化的过程之中也要表示出来,所以序列化和反序列化都需要对null的TreeNode进行特殊的处理。我是将null的地方以”*“表示,恢复的时候也要看当前节点是不是null。
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if(root==null) return "";
ArrayList<Integer> res = layerOrder(root);
StringBuilder sb = new StringBuilder();
for(int i=0;i<res.size();i++){
if(res.get(i)==null){
sb.append("*");
}else{
sb.append(res.get(i));
}
sb.append(" ");
}
sb.deleteCharAt(sb.length()-1);
System.out.println(sb.toString());
return sb.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data=="") return null;
String[] strArray = data.split(" ");
int length = strArray.length;
TreeNode root = new TreeNode(Integer.parseInt(strArray[0]));
if(length==1) return root;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
int counter =1;
while(!queue.isEmpty() && counter<length){
TreeNode node = queue.remove();
if(node!=null){
node.left = changeStringToTreeNode(strArray[counter]);
counter++;
node.right = changeStringToTreeNode(strArray[counter]);
counter++;
queue.add(node.left);
queue.add(node.right);
}
}
return root;
}
public TreeNode changeStringToTreeNode(String s){
if(s.equals("*")) return null;
else{
return new TreeNode(Integer.parseInt(s));
}
}
public ArrayList<Integer> layerOrder(TreeNode node){
ArrayList<Integer> arrayList = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(node);
while(!queue.isEmpty()){
int count = queue.size();
for(int i=0;i<count;i++){
TreeNode node1 = queue.remove();
if(node1==null){
arrayList.add(null);
}else{
arrayList.add(node1.val);
queue.add(node1.left);
queue.add(node1.right);
}
}
}
return arrayList;
}
}
Trie
* 34 实现Trie
208 Implement Trie (Prefix Tree)
https://leetcode.com/problems/implement-trie-prefix-tree/
题目要求实现Trie,重点在于Trie的值实际上是在树的“边”上,而非是节点上面。但是二叉树之中又只有节点能存储值,所以借助节点来存储其状态是否为单词已结束。
首先,实现Trie需要一个内部类Node,也需要初始化一个Node作为根节点。这个根节点之中维护着一个Node的长度为26的数组,和一个isLeaf的状态位。如果在添加的过程之中要添加哪个字母,就将相应位置上面的这个Node初始化。那么在查找的时候,如果对应位置上面的Node是null,就意味着这个单词在Trie之中还没出现。如果不是null,实际上意味的是这个边上是有值的。
所有的函数都需要辅助函数,辅助函数之中需要多加一个Node作为参数方便递归,因为每次都会将第一个字母拿走然后再递归相应的节点。
单独写了另一个辅助函数indexOfNode,用来求在数组之中的位置。
Implement a trie with
insert,search, andstartsWithmethods.Example:
Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // returns true trie.search("app"); // returns false trie.startsWith("app"); // returns true trie.insert("app"); trie.search("app"); // returns trueNote:
- You may assume that all inputs are consist of lowercase letters
a-z.- All inputs are guaranteed to be non-empty strings.
class Trie {
private class Node{
Node[] array = new Node[26];
boolean isLeaf;
}
private Node root = new Node();
/** Initialize your data structure here. */
public Trie() {
}
/** Inserts a word into the trie. */
public void insert(String word) {
insert(word,root);
}
private void insert(String word, Node node){
if(node==null) return;
if(word.length()==0) {
node.isLeaf=true;
return;
}
char c= word.charAt(0);
int index = indexOfNode(c);
if(node.array[index]==null){
node.array[index]=new Node();
}
insert(word.substring(1),node.array[index]);
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
return search(word,root);
}
public boolean search(String word, Node node){
if(node==null) return false;
if(word.length()==0) return node.isLeaf;
int index = indexOfNode(word.charAt(0));
if(node.array[index]==null) return false;
return search(word.substring(1),node.array[index]);
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
return startsWith(prefix, root);
}
public boolean startsWith(String prefix, Node node){
if(node==null) return false;
if(prefix.length()==0) return true;
int index = indexOfNode(prefix.charAt(0));
if(node.array[index]==null) return false;
return startsWith(prefix.substring(1),node.array[index]);
}
public int indexOfNode(char c){
return c-'a';
}
}
35 Trie实现求前缀和
677 Map Sum Pairs
https://leetcode.com/problems/map-sum-pairs/
本题之中借助Trie实现。两个方法:insert()和 sum()。
其中insert()是和之前一样的,只是将node之中的boolean isLeaf改成了int val。之外,没有任何改变。
但是int sum(String prefix, Node node)的改变比较大:
首先,将树递归到prefix的长度位0的时候,期间的值不计算。当prefix的值是0的时候,先将当前节点的值赋给sum,然后对其所有子节点进行递归。最后返回sum。
Implement a MapSum class with
insert, andsummethods.For the method
insert, you’ll be given a pair of (string, integer). The string represents the key and the integer represents the value. If the key already existed, then the original key-value pair will be overridden to the new one.For the method
sum, you’ll be given a string representing the prefix, and you need to return the sum of all the pairs’ value whose key starts with the prefix.Example 1:
Input: insert("apple", 3), Output: Null Input: sum("ap"), Output: 3 Input: insert("app", 2), Output: Null Input: sum("ap"), Output: 5
class MapSum {
public class Node{
Node[] array = new Node[26];
int val;
}
private Node root = new Node();
/** Initialize your data structure here. */
public MapSum() {
}
public void insert(String key, int val) {
insert(key,val,root);
}
private void insert(String key, int val, Node node){
if(node==null) return;
if(key.length()==0){
node.val = val;
return;
}
int index = indexOfChar(key.charAt(0));
if(node.array[index]==null){
node.array[index] = new Node();
}
insert(key.substring(1),val,node.array[index]);
}
public int sum(String prefix) {
return sum(prefix,root);
}
private int sum(String prefix, Node node){
if(node==null) return 0;
if(prefix.length()!=0){
Node node1 = node.array[indexOfChar(prefix.charAt(0))];
return sum(prefix.substring(1),node1);
}
int sum = node.val;
for(Node child:node.array){
sum+=sum(prefix,child);
System.out.println(prefix);
}
return sum;
}
private int indexOfChar(char c){
return c-'a';
}
}