基于参考,进行自己的解读和代码编写。
动态规划,要将问题进行转换,从底到顶的进行求解。同时,要能将状态的转换抽象出状态转移方程,将方程之间的状态流转表示出来。
先放一下学习笔记:
Lucifer 讲义笔记
1. 如何练习递归
作者在这里提出来一个观点:可以将平时的迭代写法全部变成递归写法,比如“将字符串逆序输出”。那么作者认为迭代和递归可以完成同样的功能。
public static String reverseString(String string){
if(string.length()==0) return "";
return string.charAt(string.length()-1)+reverseString(string.substring(0,string.length()-1));
}
2. 递归的坏处
递归,主要是其中存在了太多的重复计算。那么我们自然会想到,能不能先将递归过程之中的数据记录下来?动态规划之中dp数组就是起到了这个作用。
3. 动态规划
作者有一句总结:
递归是从问题的结果倒推,直到问题的规模缩小到寻常。 动态规划是从寻常入手, 逐步扩大规模到最优子结构。
动态规划的两个要素:
- 状态转移方程
- 临界条件
以爬楼梯问题为例:
70. Climbing Stairs
class Solution {
public int climbStairs(int n) {
if(n==1) return 1;
if(n==2) return 2;
int a = 1;
int b = 2;
int temp = 0;
for(int i=3;i<=n;i++){
temp = a+b;
a=b;
b=temp;
}
return temp;
}
}
下面是这个过程的查表:
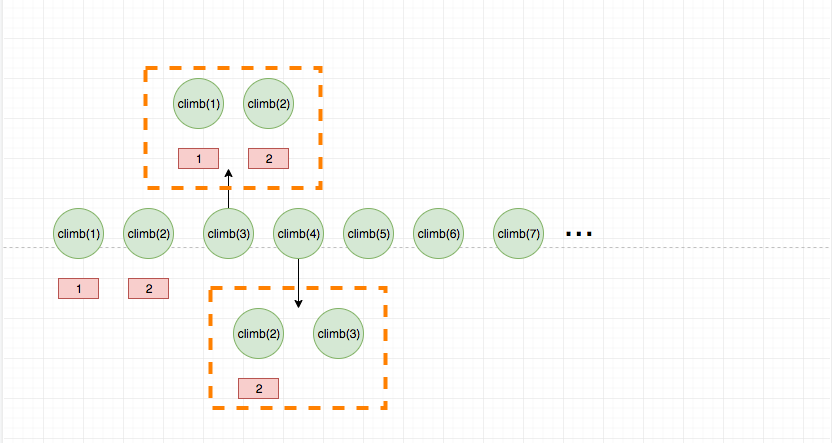
那么可能会有疑问了,这里面应该用一个一维数组来保存状态啊?因为观察可得,每一个状态都只是和之前的两个状态相关,所以这里面取巧只使用了两个变量进行存储。
如果多个状态的话,需要多维数组才可以将其完全保存。
在上面讲解的爬楼梯问题中
f(1) 与 f(2) 就是【边界】
f(n) = f(n-1) + f(n-2) 就是【状态转移公式】
4. 动态规划为什么要画表格
动态规划,从大问题着手不断去看小问题,大问题的解是和小问题关联的。到这里其实都和递归很像。
但是下面就不同了:动态规划,是使用查表的方法来缩短时间复杂度和空间复杂度。
画表格的目的,是不断的去推导,从而完成状态转移。表格之中的每一个cell都是一个小问题,填表的过程,实际上就是解决问题的过程。
先解决规模寻常的情况,就是可以直接看出来答案的情况。之后再根据这个结果逐步推导,通常表格的右下角就是问题的最大规模,也就是我们想要求解的规模。
还是参照大佬的答案:
斐波那契数列变种
1. 爬楼梯
70 Climbing Stairs (Easy)
有n阶楼梯,每次上一阶或者两阶,问有多少种方式可以上楼梯?
为了表示方便,下标从1开始,下标是几就代表上几阶。
自底向上:
- n=0,方式种类0
- n=1,方式种类1
- n=2,方式种类2
状态转移:
对于每一个台阶,其都是下一阶和下两阶的种类进行累加:dp[n]=dp[n-1]+dp[n-2]
暂存变量:
状态转移方程之中,每个状态只和两个其他状态相关,因此暂存变量两个即可。
循环次数:
0,1,2的次数都已经有了,那么从3开始循环。既然是到第n阶,那么循环应该包括第n阶。
代码:
class Solution {
public int climbStairs(int n) {
if(n<3) return n;
int pre =1,cur =2;
for(int i=3;i<=n;i++){
int sum = pre+cur;
pre = cur;
cur = sum;
}
return cur;
}
}
2. 强盗抢劫,不可抢相邻屋子
198 House Robber
自底向上:
- nums.length==0:没有数组,抢不到
- nums.length==1:只有一户,就抢他
- nums.length==2:有两户,抢多的
状态转移方程:
对于每一个屋子,要么是抢其之前的+这个屋子,要么抢比其小一号的屋子:
dp[i]=Math.max(dp[i-2]+nums[i-1],dp[i-1)
暂存变量:
可以看出每次和状态来说,只和其之前的两个状态相关,因此只要保存之前的两个状态
循环次数:
从3开始,自然也还是要包括本身
class Solution {
public int rob(int[] nums) {
if(nums.length==0) return 0;
if(nums.length==1) return nums[0];
if(nums.length==2) return Math.max(nums[0],nums[1]);
int cur = Math.max(nums[0],nums[1]),pre = nums[0];
for(int i=3;i<=nums.length;i++){
int sum = Math.max(pre+nums[i-1],cur);
pre = cur;
cur = sum;
}
return cur;
}
}
##